

풀이
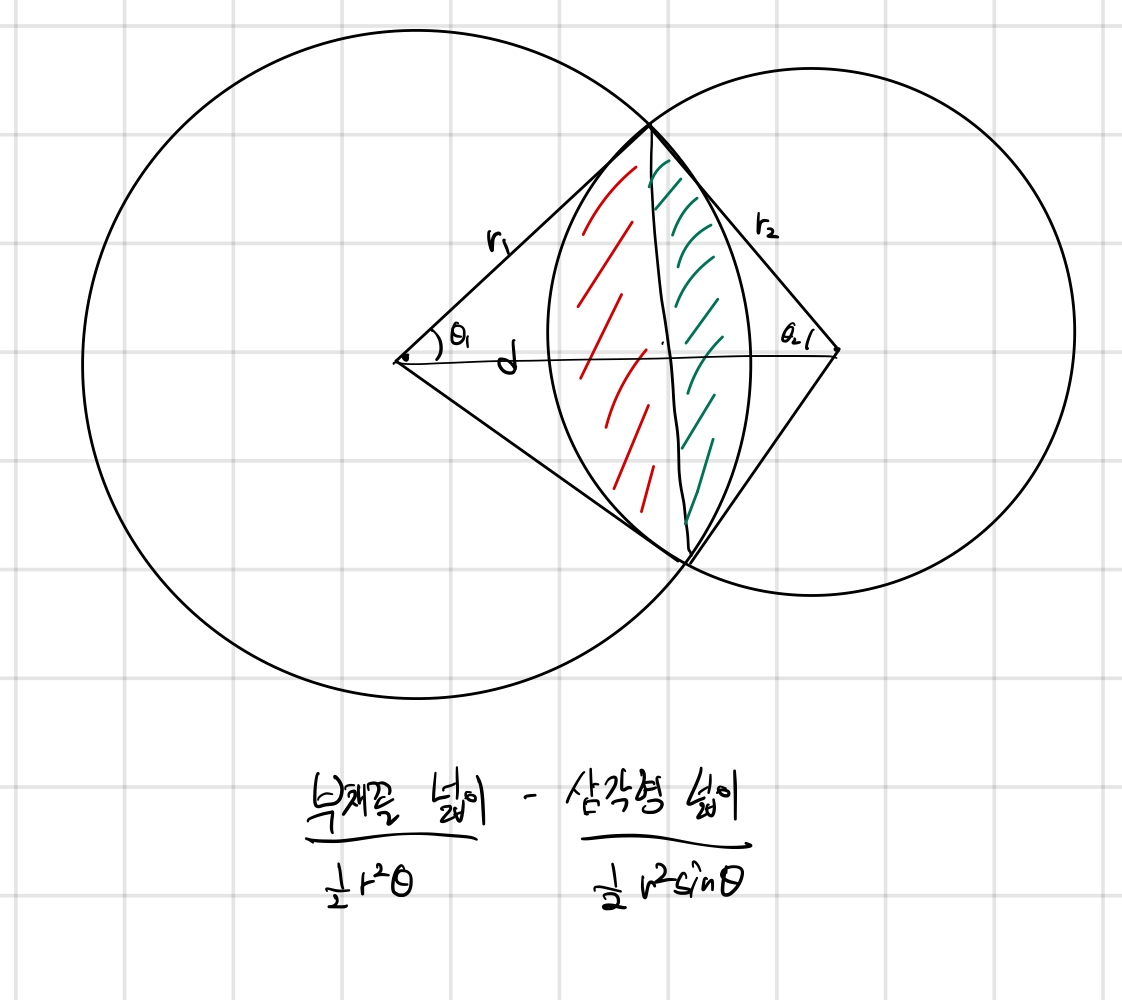
위의 그림과 같이 두 원의 겹친부분 넓이는 부채꼴의 넓이 - 삼각형의 넓이로 구할 수 있다. θ값은 코사인법칙으로 구할 수 있다
코드
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
double sqare(double a) {
return a * a;
}
int main() {
double x1, y1, r1, x2, y2, r2; scanf("%lf %lf %lf %lf %lf %lf", &x1, &y1, &r1, &x2, &y2, &r2);
if (r1 < r2) {
swap(x1, x2);
swap(y1, y2);
swap(r1, r2);
}
double d = sqrt(sqare(x1 - x2) + sqare(y1 - y2));
if (d >= r1 + r2) { // 겹치지 않는 경우
printf("0.000");
} else if (d + r2 <= r1) { // 작은원이 큰원 내부에 있는 경우
printf("%.3lf", r2 * r2 * acos(-1));
} else {
//코사인법칙
double theta1 = acos((sqare(r1) + sqare(d) - sqare(r2)) / (2 * r1 * d));
double theta2 = acos((sqare(r2) + sqare(d) - sqare(r1)) / (2 * r2 * d));
double s1 = (r1 * r1 * theta1) - (r1 * r1 * sin(2 * theta1)) / 2;
double s2 = (r2 * r2 * theta2) - (r2 * r2 * sin(2 * theta2)) / 2;
printf("%.3lf", s1 + s2);
}
}'Algorithm > BOJ' 카테고리의 다른 글
| 백준[11723] 집합 (0) | 2021.07.03 |
|---|---|
| 백준[1069] 집으로 (0) | 2021.07.01 |
| 백준[2162] 선분 그룹 (0) | 2021.06.30 |
| 백준[17387] 선분 교차 2 (0) | 2021.06.30 |
| 백준[20149] 선분 교차 3 (0) | 2021.06.29 |