
백준[20149] 선분 교차 3
2021. 6. 29. 23:12
Algorithm/BOJ
풀이 이 문제는 선행 문제인 선분교차 2 이 문제를 풀었다면 어렵지 않다. 이 문제를 모른다면 여기를 참고하자. 위의 문제를 이해했다고 가정하고 설명하겠다. 이 문제는 선분 교차 2에서 교점의 좌표만 추가로 구하면 된다. 교점의 좌표는 두 점으로부터 직선의 방정식 두 개를 구한 후 연립하면 된다. 이때 직선이 y축과 평행할 때를 조심해야 한다. 나는 이 것을 간과해 맞왜틀을 외치다 질문검색을 들어가 봤다. 코드 #include #include #define x first #define y second using namespace std; using ll = long long; using pll = pair; ll ccw(pll a, pll b, pll c) { ll ret = a.x * b.y + b.x..

백준[1949] 우수마을
2021. 6. 29. 18:10
Algorithm/BOJ
풀이 방법 이 문제는 트리 + dp를 이용하는 문제이다. dp는 dp[현재 노드 번호][현재 노드가 우수인지 아닌지 여부]로 정의한다. 2번 조건에 의해 현재 노드가 우수 마을이면 항상 다음 노드는 우수 마을이 아니고, 우수마을이 아니라면 다음 노드는 우수마을일수도 있고 아닐 수도 있다. 3번 조건은 1번 조건에 의해 자연스럽게 만족된다. 우수x -> 우수x -> 우수x 이런식으로 계속해서 될 수 있다고 착각을 하여 시간을 많이 뺏겼다. 하지만 우수x -> 우수x -> 우수x 이 상황은 항상 올 수 없다. 왜냐하면 우수x -> 우수x -> 우수x 이 상황보다 우수x -> 우수 -> 우수x 이 상황이 항상 더 크기 때문에 최댓값을 유지하기 위해서는 우수x가 계속해서 올 수 없다. 코드 #include #i..

백준[2533] 사회망 서비스(SNS)
2021. 6. 24. 13:26
Algorithm/BOJ
풀이 방법 이 문제는 트리에서 dp를 이용하는 문제이다. dp[현재 노드][현재 노드가 얼리어답터인가 여부]로 dp테이블을 만들고 현재 노드가 얼리어답터가 아니라면 자식노드는 항상 얼리어답터이고, 얼리어답터라면 얼리어답터일수도, 아닐수도 있다. 이 문제는 이 문제 와 매우 비슷하여 쉽게 해결하였다. 코드 #include using namespace std; vector v, tree; int dp[1000006][2]; bool visited[1000006]; //단방향 그래프로 바꾼다 void dfs(int cur) { if (visited[cur]) return; visited[cur] = true; for (auto nxt : v[cur]) { if (!visited[nxt]) { tree[cur]..

백준[2213] 트리의 독립집합
2021. 6. 24. 11:31
Algorithm/BOJ
풀이 방법 이 문제는 트리에서의 dp문제 이다. 저는 맞왜틀을 외치다 여기 를 참고했습니다. 우선 dfs를 이용하여 임의의 루트를 정하여 그 트리의 경로를 저장합니다. dp정의는 dp[현재 노드][현재 노드를 포함하는가 여부]로 정의하고, 만약 현재 노드를 포함한다면 자식 노드는 포함 할 수 없고, 포함하지 않는다면 자식노드를 포함하든 안하든 상관이 없다. 포함하는 경로 추적은 루트 노드부터 시작해서 dfs를 돌며 dpf를 돌때 저장한 배열의 값이 true인 경우를 ans배열에 저장한다. 코드 #include #include #include using namespace std; int cost[10004], dp[10004][2], check[10004], res; vector v, tree; vecto..

백준[2887] 행성터널
2021. 6. 22. 21:17
Algorithm/BOJ
풀이 방법 모든 간선에 대해 크루스칼 알고리즘을 이용하면 간선의 개수가 N * (N - 1) / 2이기 때문에 메모리 초과가 발생한다. 그렇기 때문에 모든 간선에 대해 크루스칼 알고리즘을 적용하는 것이 아닌 x로 정렬하여 인접한 노드들 끼리의 간선, y로 정렬한 간선, z로 정렬한 간선들로만 크루스칼 알고리즘을 적용한다. 코드 #include #include #include #include using namespace std; using pii = pair; using piii = pair; struct T { int x, y, z, idx; }; priority_queue pq; int N, ans, cnt; T arr[100005]; int par[100005]; bool compare(T a, T ..

백준[1774] 우주신과의 교감
2021. 6. 22. 15:35
Algorithm/BOJ
풀이 방법 크루스칼 알고리즘을 이용하여 풀이한다. 이미 연결 된 간선은 미리 연결해놓고 가장 거리가 짧은 간선을 뽑아 사이클이 있는지 확인하고 연결한다. 코드 우선순위큐를 이용한 구현 #include #include #include #include #include using namespace std; using ll = long long; using pll = pair; using pdll = pair; pll arr[1003]; ll N, M, par[1003], cnt, lev[1003]; priority_queue pq; ll dist(pll a, pll b) { return (a.first - b.first) * (a.first - b.first) + (a.second - b.second) * (..
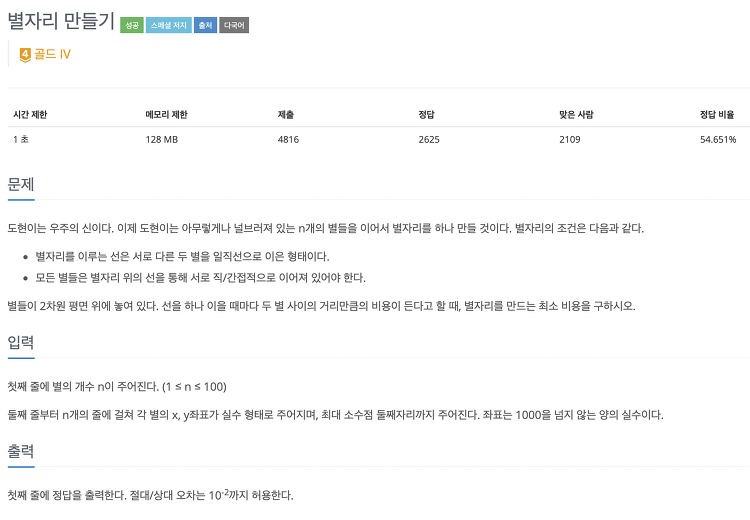
백준[4386] 별자리 만들기
2021. 6. 22. 00:39
Algorithm/BOJ
풀이 방법 최소 신장 트리(MST)를 구하는 문제이다. MST는 prim 알고리즘과 kruskal 알고리즘을 통해 구할 수 있다. 이 풀이는 prim 알고리즘을 이용했다. cf) prim 알고리즘을 모른다면 여기를 참고하세요 코드 #include #include #include using namespace std; using pdd = pair; using pdi = pair; pdd arr[102]; bool visited[102]; priority_queue pq; // 최소 힙 int N; double ans; //점과 점 사이의 거리 double dist(pdd a, pdd b) { return sqrt((a.first - b.first) * (a.first - b.first) + (a.secon..
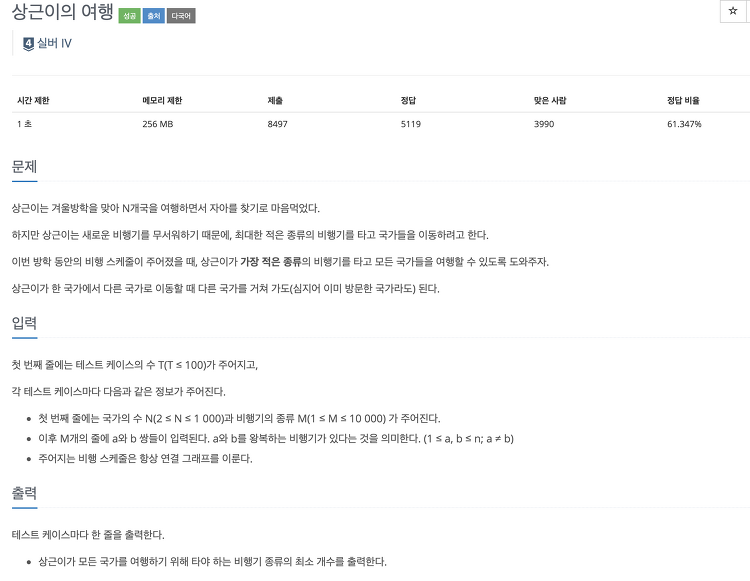
백준[9372] 상근이의 여행
2021. 6. 21. 23:54
Algorithm/BOJ
풀이 방법 spanning tree의 간선의 개수를 구하는 간단한 dfs 문제다. spanning tree의 간선의 개수는 dfs 또는 bfs 탐색 중 사용하는 간선을 모으면 된다. 코드 #include #include #include using namespace std; bool visited[1003]; vector v; int ans; void dfs(int s) { visited[s] = true; ans++; for (auto i : v[s]) { if (!visited[i]) dfs(i); } } int main() { int T; scanf("%d", &T); while (T--) { int N, M; scanf("%d %d", &N, &M); v.clear(); v.resize(N + 1)..
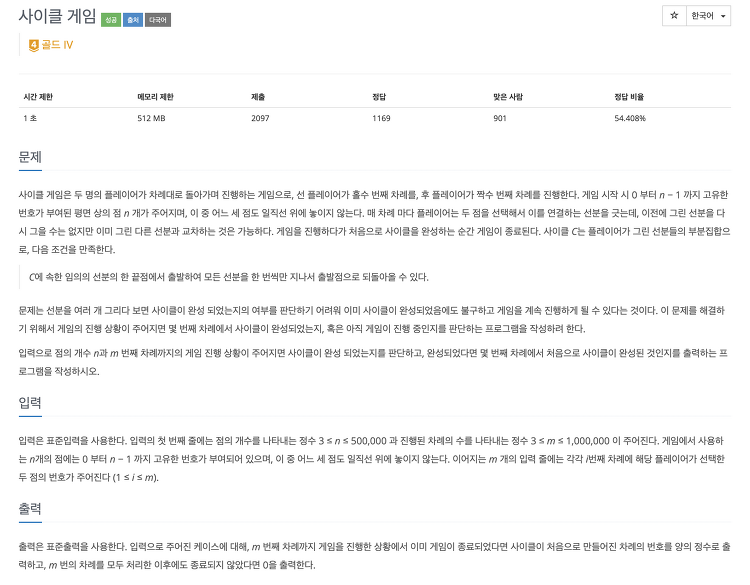
백준[20040] 사이클게임
2021. 6. 21. 23:26
Algorithm/BOJ
풀이 방법 유니온 파인드라는 자료구조를 이용하여 풀이하였다. 입력받은 두개의 루트 노드가 같으면 사이클이 형성되었다고 판단하고, 다르다면 두개의 트리를 합친다. 코드 #include #include using namespace std; int par[500005], level[500005]; int find(int x) { if (x == par[x]) return x; return par[x] = find(par[x]); } void merge(int x, int y) { int a = find(x), b = find(y); if (a == b) return; if (level[a] > level[b]) swap(a, b); if (level[a] == level[b]) level[b]++; par[a..

백준[2629] 양팔저울
2021. 5. 3. 22:19
Algorithm/BOJ
풀이 방법 dp[i][j] : i번째 추까지 사용했을 때 무게 j를 만들 수 있는지 여부 i번째 상태는 i - 1번째 상태에 i번째 무게만큼 더할 것인지 뺄 것인지 아무것도 안 할 것인지로 정의할 수 있다. 코드 무게가 음수인 경우를 커버하기 위해 40000을 기본값으로 했다. #include int weight[32]; bool dp[32][80004]; int main() { int N; scanf("%d", &N); for (int i = 1; i