
백준[1069] 집으로
2021. 7. 1. 17:39
Algorithm/BOJ
풀이 이 문제는 별다른 알고리즘 사용없이 모든 케이스를 잘 생각해야하는 문제다. 케이스는 5가지가 있다. 1. 그냥 걸어가는 경우 2. 점프하고 남은 거리 걷는 경우 3. (0, 0)을 넘어서까지 한번 더 점프하고 뒤로 걷는 경우 4. 방향을 꺾어서 j + 1 번 점프하는 경우 5. 점프만 두번 하는 경우 코드 #include #include #include using namespace std; int main() { int x, y, d, t; scanf("%d %d %d %d", &x, &y, &d, &t); double dist = sqrt(x * x + y * y); int jump = dist / d; double remain = dist - jump * d; //그냥 걷는 경우, 점프 하고 남..

백준[7869] 두 원
2021. 6. 30. 21:08
Algorithm/BOJ
풀이 위의 그림과 같이 두 원의 겹친부분 넓이는 부채꼴의 넓이 - 삼각형의 넓이로 구할 수 있다. θ값은 코사인법칙으로 구할 수 있다 코드 #include #include #include using namespace std; double sqare(double a) { return a * a; } int main() { double x1, y1, r1, x2, y2, r2; scanf("%lf %lf %lf %lf %lf %lf", &x1, &y1, &r1, &x2, &y2, &r2); if (r1 = r1 + ..
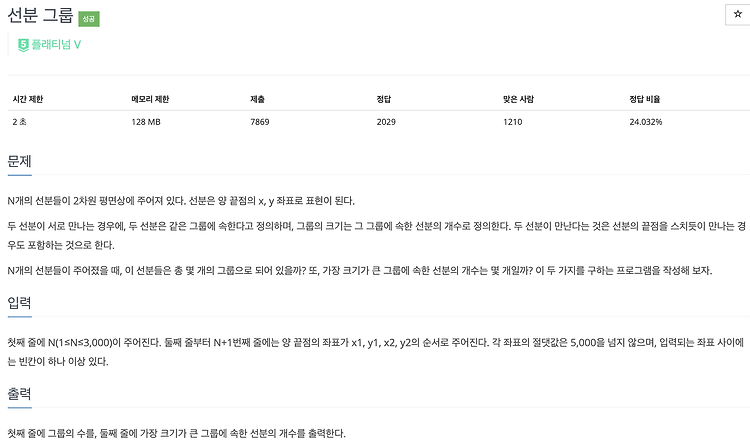
백준[2162] 선분 그룹
2021. 6. 30. 20:19
Algorithm/BOJ
풀이 이 문제는 ccw와 union find를 이용하여 해결 할 수 있다. 두 직선이 교차되었는지 판별은 선분 교차2와 동일하다. 모든 선분들에 대해 서로 교차되었는지 판변하고 교차되었다면 union을 한다. ccw의 리턴값을 1 -1 0이 아닌 원래 값으로 리턴하여, check함수에서 두 값을 곱할 시 오버플로우가 발생할 것을 예상하지 못하고 맞왜틀을 외쳤다. 조심하도록 하자. 코드 #include #include #define x first #define y second using namespace std; using pii = pair; pii a[3003], b[3003]; int par[3003], member_size[3003]; int ccw(pii a, pii b, pii c) { int ..

백준[17387] 선분 교차 2
2021. 6. 30. 20:11
Algorithm/BOJ
풀이 선분의 교차는 ccw의 값으로 구한다. ccw를 모른다면 여기를 참고하자. 직선이 교차하기 위해서는 abc abd의 ccw값의 부호가 다르고, cda cdb의 값의 부호도 달라야한다. 직선이 겹치는 경우는 항상 a b) swap(a, b); if (c > d) swap(c, d); return a

백준[20149] 선분 교차 3
2021. 6. 29. 23:12
Algorithm/BOJ
풀이 이 문제는 선행 문제인 선분교차 2 이 문제를 풀었다면 어렵지 않다. 이 문제를 모른다면 여기를 참고하자. 위의 문제를 이해했다고 가정하고 설명하겠다. 이 문제는 선분 교차 2에서 교점의 좌표만 추가로 구하면 된다. 교점의 좌표는 두 점으로부터 직선의 방정식 두 개를 구한 후 연립하면 된다. 이때 직선이 y축과 평행할 때를 조심해야 한다. 나는 이 것을 간과해 맞왜틀을 외치다 질문검색을 들어가 봤다. 코드 #include #include #define x first #define y second using namespace std; using ll = long long; using pll = pair; ll ccw(pll a, pll b, pll c) { ll ret = a.x * b.y + b.x..