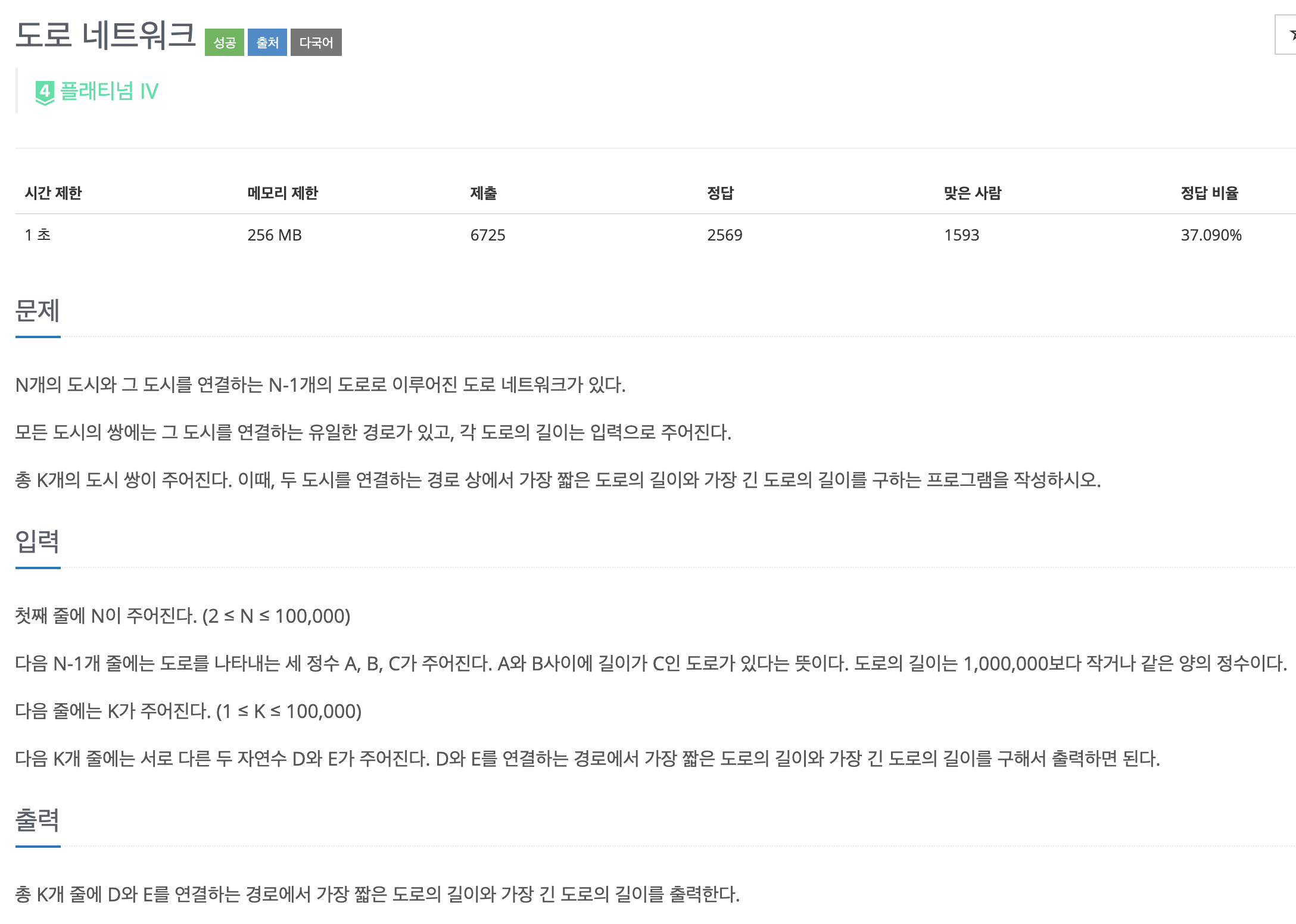

문제 링크
https://www.acmicpc.net/problem/3176
풀이
이 문제는 LCA를 이용한 문제이다. 쿼리당 O(logN)에 LCA를 처리하는 방법을 모른다면 LCA2부터 공부하는 것이 좋다.
이 글은 LCA2를 모두 이해했다고 가정하고 설명하겠다.
이 문제는 LCA를 구하는 과정에서 부분 최댓값과 최솟값을 O(1)에 구할 수 있어야 한다.
그러기 위해서는 sparse table을 이용하여 전처리를 해줘야 한다.
부분 최댓값과 최솟값을 구하는 전처리 코드는 아래와 같고 O(NlogN)에 처리할 수 있다.
for (int j = 1; j <= 20; j++) {
for (int i = 1; i <= n; i++) {
pmax[i][j] = max(pmax[i][j - 1], pmax[par[i][j - 1]][j - 1]);
pmin[i][j] = min(pmin[i][j - 1], pmin[par[i][j - 1]][j - 1]);
}
}이렇게 부분 최대, 최솟값을 미리 구해놓은 다음 LCA를 구할 때 부모로 올라가며 최대 최솟값을 갱신시켜주면 답을 구할 수 있다.
cf) 27~30행 36~39행에서 x, y값을 사용하는데 x, y값을 바꾼 후 바뀐 x, y 값을 이용하여 rmax, rmin값을 갱신하는 실수를 하여 시간을 많이 잡아먹었다. 이런 사소한 실수가 디버깅하기 정말 까다로운 것 같다. 앞으로 조심하자.
코드
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
using pii = pair<int, int>;
vector<pii> v[100005];
int par[100005][22], lev[100005], pmax[100005][22], pmin[100005][22];
void dfs(int cur, int prv) {
par[cur][0] = prv;
lev[cur] = lev[prv] + 1;
for (auto nxt : v[cur]) {
if (prv != nxt.first) {
pmax[nxt.first][0] = nxt.second;
pmin[nxt.first][0] = nxt.second;
dfs(nxt.first, cur);
}
}
}
pii query(int x, int y) {
int rmax = -1e9, rmin = 1e9;
if (lev[x] > lev[y]) swap(x, y);
for (int i = 20; i >= 0; i--) {
if (lev[y] - lev[x] >= (1 << i)) {
rmax = max(rmax, pmax[y][i]);
rmin = min(rmin, pmin[y][i]);
y = par[y][i];
}
}
if (x == y) return {rmin, rmax};
for (int i = 20; i >= 0; i--) {
if (par[x][i] != par[y][i]) {
rmax = max(rmax, max(pmax[x][i], pmax[y][i]));
rmin = min(rmin, min(pmin[x][i], pmin[y][i]));
x = par[x][i];
y = par[y][i];
}
}
rmax = max(rmax, max(pmax[x][0], pmax[y][0]));
rmin = min(rmin, min(pmin[x][0], pmin[y][0]));
return {rmin, rmax};
}
int main() {
int n; scanf("%d", &n);
for (int i = 0; i < n - 1; i++) {
int a, b, c; scanf("%d %d %d", &a, &b, &c);
v[a].push_back({b, c});
v[b].push_back({a, c});
}
dfs(1, 0);
for (int j = 1; j <= 20; j++) {
for (int i = 1; i <= n; i++) {
par[i][j] = par[ par[i][j - 1] ][j - 1];
pmax[i][j] = max(pmax[i][j - 1], pmax[par[i][j - 1]][j - 1]);
pmin[i][j] = min(pmin[i][j - 1], pmin[par[i][j - 1]][j - 1]);
}
}
int k; scanf("%d", &k);
while (k--) {
int a, b; scanf("%d %d", &a, &b);
auto [m, M] = query(a, b);
printf("%d %d\n", m, M);
}
}
'Algorithm > BOJ' 카테고리의 다른 글
| 백준[2150] Strongly Connected Compoment (0) | 2021.07.28 |
|---|---|
| 백준[13511] 트리와 쿼리 2 (0) | 2021.07.25 |
| 백준[11438] LCA 2 (0) | 2021.07.24 |
| 백준[17435] 합성함수와 쿼리 (0) | 2021.07.23 |
| 백준[3584] 가장 가까운 최소 공통 조상 (0) | 2021.07.23 |